Psychology 230

Probability

I. Introduction to Probability

Two jars of marbles—Jar A (population) contains 50 black and 50 white.  Jar B (another population) contains 90 black and 10 white marbles. 

A. Inferential Statistics

B. Definition—a fraction or proportion for any particular outcome. 

Probability of A = # outcomes classified as A/total # possible outcomes

C. Zero Probability--An event that never occurs has a probability of zero.  However, a probability of zero does not mean that event is guaranteed never to occur. 

 D. Random Sampling —process that must be used to obtain the outcomes in order to fulfill the definition of probability.

Requirements of a random sample: (1) Each individual in the population has an equal chance of being selected and (2) There must be constant probability when more than one individual is to be selected.

E. Frequency Distributions  

Can determine a probability from a frequency distribution table by computing the proportion for the X value in question.  p=f/n

Because probability and proportion are equivalent, a particular proportion of the frequency distribution graph corresponds to a particular probability in the population.

 

II. Probability and the Normal Distribution

 

A. Characteristics of the Normal Distribution:

-        Symmetrical

-        Mean=Median

-        Most scores fall around the mean

-         Extreme high or low scores are relatively rare

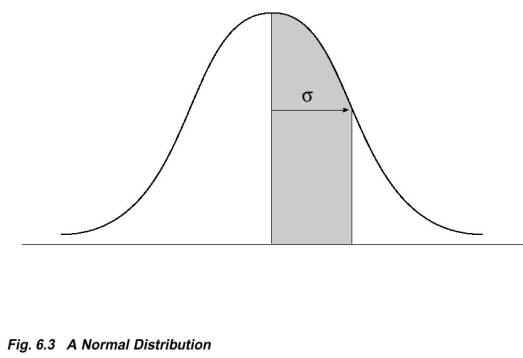
A distribution is normal only if it has the following proportions:

B. Answering Probability Questions

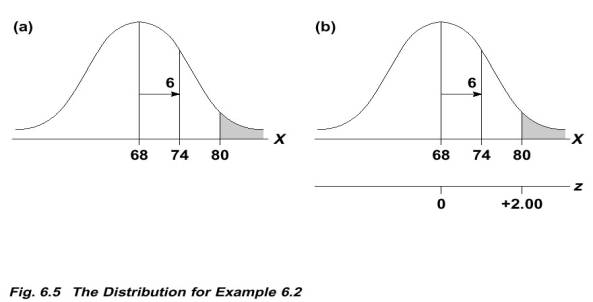
Adult heights are normally distributed with μ = 68 and σ = 6.  What is the probability of randomly selecting an individual from this population who is taller than 6 feet 8 inches (X=80 inches)?

  Out of all possible adult heights, what proportion is greater than 80?

 (refer to graph above)

so proportion is .0228. 

Drawback:  Shows proportions for only whole-number z-score values.

C. The Unit Normal Table

Lists proportions of the normal distribution for a full range of possible z-scores (G&W p. 725-728).

For any z-score value, the proportions in columns B and C will always add to 1.00.  

Distribution is symmetrical so the proportions on the right-hand side are exactly the same as the corresponding proportions on the left-hand side.

Z-score values will change signs (+ and -) from one side tot he other, but the proportions will be the same and will always be positive.

D. Answering questions with the unit normal table

Sketch the distribution and shade in the area you are trying to determine.

Look up the appropriate value of z in the unit normal table.

Note: sometimes no column in the unit normal table directly gives the answer we need, so must do some math.

What proportion of the normal distribution corresponds to the tail beyond z = -0.50?  The proportion in the left tail beyond z = -0.50 is the same as the proportion in the right tail beyond z = +0.50.  Look up z = .50 in column A, and find the proportion in tail (column C).  p(z<-0.50) = .3085 or 30.85%

What proportion of the scores fall between z = -0.40 and z = +1.25?  No column in the table directly gives us the answer.  The area that we do NOT want consists of the two tails.  The solution is to subtract both of these proportions from 1.00 (100%).  For z = -0.40, the tail entry is .3446 and for z = +1.25, the tail entry is .1056.

 

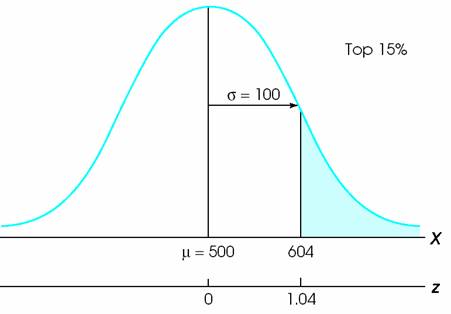
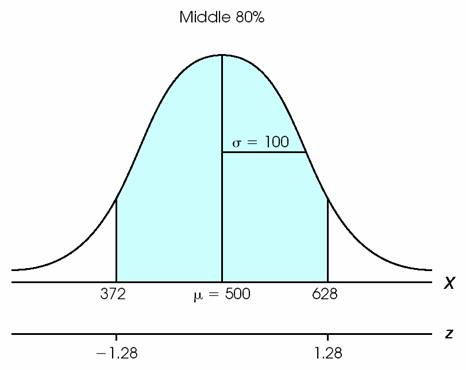
Figure 6.13  (p. 179)  The distribution of SAT scores. The problem is to locate the score that separates the top 15% from the rest of the distribution. A line is drawn to divide the distribution roughly into 15% and 85% sections.
 

 

Figure 6.14  (p. 180)  The distribution of SAT scores. The problem is to find the scores that determine the middle 80%.

III. Percentiles, Percentile Ranks, and Quartiles

A. Percentile Rank - % of scores in distribution less than or equal to X . When finding percentile ranks, we will always be concerned with the percentage on the left-hand side of an X value (which must first be converted to a z-score).

B. Percentile - the particular score (X) associated with a percentile rank. You are given a percentage (a percentile rank) and you must find the corresponding X value.  Must first determine the z-score that corresponds to the proportion given.

For example, suppose you have a score of x = 43 on an exam. You know that exactly 60% of the class had scores of 43 or lower. Then your score x = 43 has a percentile rank of ______ and the score x= _____ would be called the 60th percentile.

C. Calculate Examples

D. Quartiles - Q1, Q2, and Q3  

The area in a distribution can be divided into four equal parts called quartiles, each corresponding to 25%.  Q1 is the score that separates the lowest 25% (one-quarter) of the distribution from the rest.  Q2 is the score that separates the lowest 50% (two-quarters).  Q3 is the score that separates the lowest 75% (three-quarters) of the distribution from the rest.

 

For a normal distribution, Q1, Q2, & Q3 always correspond to:

     

        E. Calculate Examples

IV.  The Binomial Distribution

A. two categories

- men/women

- head/tails

- selected/not selected

- categories called: A and B

Figure 6.17  (p. 184)  The relationship between the binomial distribution and the normal distribution. The binomial distribution is always a discrete histogram, and the normal distribution is a continuous, smooth curve. Each X value is represented by a bar in the histogram or a section of the normal distribution.
 

 

B. Nomenclature
for any one trial:
        - prob (A) = p

- prob (B) = q

- p + q = 1

across multiple trials:
- # observations = n

- X = # of A in observations (n)

- Mean:

m = pn

- Standard Deviation:

s = sqrt(npq)

- use z formula (below) and tables as before

 

C. Use when pn >= 10, and qn >= 10

(if either is smaller this is not appropriate test)